Een bewijs zonder woorden voor de som van de derdemachten van de eerste n positieve gehele getallen.

De driehoekgetallen zijn 1, 3, 6, 10, 15, ... en het n-de driehoeksgetal is Tn = n(n + 1)/2.
De som van twee opeenvolgende driehoeksgetallen is steeds een kwadraatgetal, nl. (n – 1)(n + 1)/2 + n(n + 1)/2 = n².
Hieronder staat een bewijs zonder woorden (gemakkelijk te veralgemenen).

(F1)² + (F2)² + (F3)² + ... (Fn)² = Fn x Fn+1
(met F1 = 1, F2 = 1, F3 = 2 enz ...)
Zo is bijvoorbeeld voor n = 4: 1² + 1² + 2² + 3² = 3 x 5
en voor n = 5: 1² + 1² + 2² + 3² + 5² = 5 x 8
en voor n = 6: 1² + 1² + 2² + 3² + 5² + 8² = 8 x 13.
Hieronder zien we een bewijs voor n = 7.
En zie je in dat je aan de hand van een dergelijke tekening
eigenlijk ook een algemeen 'bewijs zonder woorden' hebt gegeven?

Hieronder staat een bewijs voor de formule voor de 'oneindige som' (meetkundige reeks)
a + ar + ar² + ar³ + ... (a verschillend van nul en 0 < r < 1)
en ook nog drie bijzondere gevallen ervan.


1/4 + 1/16 + 1/64 + ... = 1/3

1/3 + 1/9 + 1/27 + ... = 1/2

3/4 + 3/16 + 3/64 + ... = 1

________________________________________________________________________________________________________________________________________
Hieronder staat een bewijs zonder woorden voor de formule
1 + 3 + 5 + ... + (2n – 1) + (2n + 1) + (2n – 1) + ... + 5 + 3 + 1 = n2 + (n + 1)2.

1 = 1³
3 + 5 = 2³
7 + 9 + 11 = 3³
3 + 15 + 17 + 19 = 4³
enzovoort ...
Ook hiervoor hebben we een bewijs zonder woorden.

En kan je ook nog aantonen dat de onderstaande som gelijk is aan 1?
We geven een bewijs zonder en een bewijs met woorden.



Hieronder staat nog een toepassing met 'gnomons' (met een bewijs zonder woorden).
Merk op dat 1 + 3 + 5 + ... + (2n – 1) = n²
en 1 + 3 + 5 + ... + (4n – 1) =(2n)² = 4n²
en bijgevolg is (2n + 1) + (2n + 3) + ... + (4n – 1) = 3n².

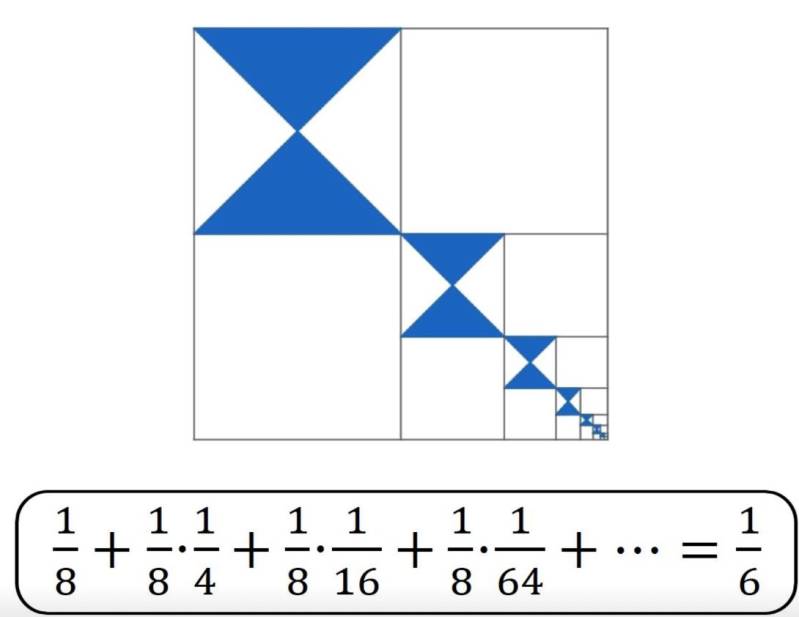
VERDUIDELIJKING.
In het vierkant linksboven is de helft gekleurd; dat is dus 1/8-ste van de totale figuur.
Daaronder is 1/8-ste gekleurd van 1/4-de, dan 1/8-ste van 1/16-de enzovoort ...
Anders bekeken: in het vierkant linksboven is de helft gekleurd en dat is bijgevolg 1/6-de van de figuur die bestaat uit dat vierkant en de (niet-ingekleurde) vierkanten ernaast en eronder. Dit procédé wordt herhaald zodat uiteindelijk 1/6-de van de totale figuur is gekleurd.


Maak jouw eigen website met JouwWeb